La geometria iperbolica

1. Le ipotesi di Saccheri

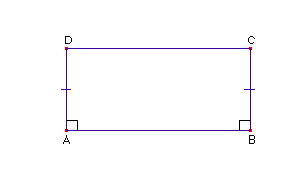
Considerato un quadrilatero ABCD con gli angoli in A e in B retti, i lati AD e BC di uguale lunghezza, Saccheri, sempre a prescindere dal 5° postulato di Euclide, dimostra che anche gli angoli in C e in D sono uguali fra loro e quindi  presenta le seguenti tre possibilità:

I)     angoli in C e D retti  (R)                      

II)      angoli in C e D  ottusi

III)     angoli in C e D acuti

 Nell'ipotesi II, risulta  CD < AB

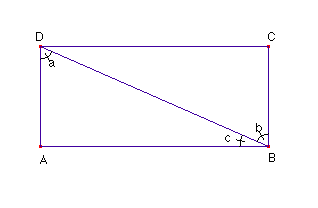
Ne segue che l'angolo a è maggiore dell'angolo b (due lati dei triangoli sono fissati e si considera l'angolo compreso) e, poichè c + b = R, la somma degli angoli del triangolo ABD risulta > 2R, contro il completamento alla PROP.17.
L'ipotesi è quindi scartata.

Nell'ipotesi III, risulta  CD > AB e quindi l'angolo a minore dell'angolo b; di conseguenza la somma degli angoli del triangolo ABD è < 2R.

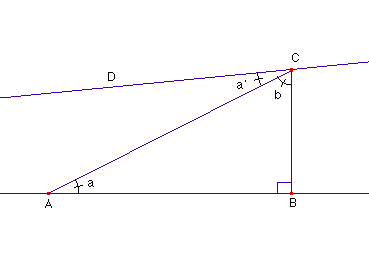
In tal caso, considerato il triangolo rettangolo ABC, egli costruisce CD con a' = a, in modo che, per la PROP.28, la retta AB risulta parallela alla retta CD; ma, essendo all'interno dell'ipotesi III, dell'angolo acuto, ottiene a + b < R e quindi a' + b < R. Risultano quindi due rette, una perpendicolare e l'altra obliqua a una stessa retta BC, che non si incontrano!
In base a quanto precede, il Saccheri stabilisce l'esistenza di due rette p e q, a sinistra e a destra di C, le quali dividono il fascio di rette per C in due parti: quella con le rette che intersecano AB e quella con le rette che hanno con essa una perpendicolare in comune (pur non intersecandola).
A questo punto, egli ritiene quanto ottenuto contrario all'intuitiva conoscenza della linea retta e respinge anche l'ipotesi in questione.

In definitiva, accetta la prima possibilità come unica possibile sulla base dei precedenti assiomi o postulati e, di conseguenza, pensa di avere, in questo modo, dimostrato il 5° postulato euclideo (in realtà assumendo un enunciato equivalente).



2. Il modello di Klein della geometria iperbolica

La prova del ragionamento scorretto del Saccheri, che involontariamente ha di fatto costruito alcune proposizione di geometria non euclidea iperbolica, è data dalla costruzione di un modello di tale geometria all'interno della stessa geometria euclidea, come è stato fatto dal matematico Felix Klein: tale modello soddisfa tutti gli assiomi (postulati) di Euclide, escluso il quinto, quello delle parallele (che è negato, risultando l'esistenza, per un punto non appartenente a una data retta, di più di una retta parallela ad essa).
In tal modo è provato che la nuova geometria è coerente, cioè non contradditoria, se tale è la geometria euclidea (perchè, come adesso si vedrà, si trasferiscono solo i termini in un nuovo contesto) e che il quinto postulato non può essere dedotto dagli altri assiomi euclidei, perchè altrimenti risulterebbe valido anche nel modello.

Klein considera come piano l'insieme dei punti interni ad un cerchio e ciascuno di questi è visto come punto non euclideo.
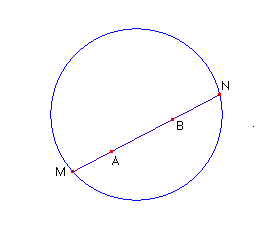
Ogni corda del cerchio (esclusi gli estremi) è considerata una retta non euclidea.
Due corde che hanno un estremo in comune (sulla circonferenza e quindi non si intersecano) costituiscono due rette parallele.
Per due punti passa sempre una retta (vale a dire, per due punti interni al cerchio passa sempre una corda).
Data una retta e un punto fuori di essa, le rette del fascio di centro questo punto si dividono in un insieme di secanti e in uno di non secanti (rette iperparallele): le rette parallele di cui sopra sono quelle che separano i due insiemi.
Le isometrie (movimenti o congruenze non euclidee) vengono definite come particolari trasformazioni (proiettive) che mutano il cerchio in se stesso (i punti interni, pur potendo cambiare posizione, rimangono interni e analogamente i punti sulla circonferenza rimangono su di essa),
mentre la distanza (non euclidea) tra due punti A e B, data da: