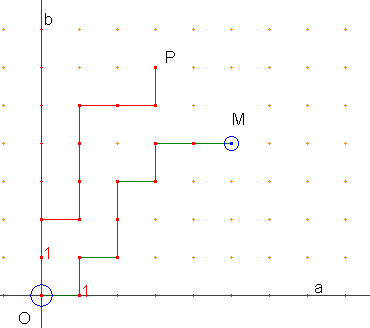
Calcolo combinatorio

Dal punto O iniziamo una camminata casuale in una città (in figura è schematizzata la zona, un tratto di isolato corrispondendo a un lato di un quadretto, procedendo nel modo seguente:
a ogni bivio lanciamo una moneta: se viene TESTA prendiamo il tratto di destra, altrimenti procediamo in avanti (allontanandoci sempre dalle rette a o b.
Qual è la probabilità, dopo 9 lanci della moneta, di trovarsi nel punto M, dove è situato un interessante monumento, distante da O 9 tratti di isolato ?

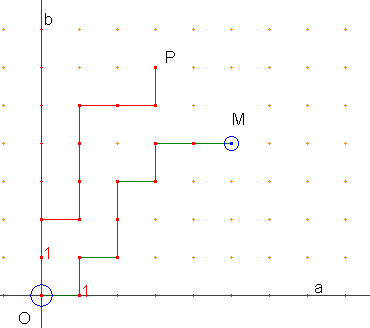
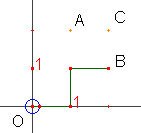
1. Gli schemi seguenti mostrano che sono 3 i percorsi che conducono al punto B (ciascuno formato da 3 tratti):

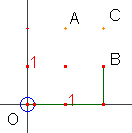
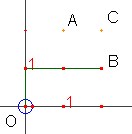
Quanti sono i percorsi che conducono ad A ?
Quanti quelli che conducono a C?
Si può determinare rapidamente il numero dei percorsi che conducono a C, conoscendo il numero di quelli che conducono ad A e a B?

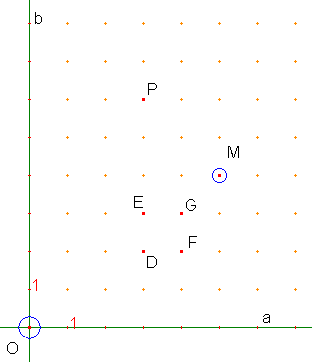
Con riferimento allo schema precedente, calcolate il numero dei percorsi che conducono a D, E, F, G.
Osservate che, ad esempio, i percorsi che arrivano a G  sono quelli che arrivano da E o da F, quindi è possibile adottare una strategia per calcolare rapidamente, partendo da O, il numero dei percorsi in ogni punto.

Calcolate infine il numero di quelli che conducono a M.

Il punto P è raggiungibile con 9 lanci della moneta, ma non può più condurre a M.
Segnate tutti i punti raggiungibili con 9 lanci e calcolate il numero dei percorsi per ciascuno di essi.

Dividendo il numero dei percorsi favorevoli per quello di tutti i percorsi possibili (con 9 tratti) potete ottenere la probabilità richiesta:

                                                           

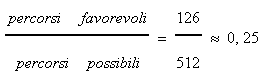
2. Potenza di un binomio
 

Come sappiamo,
                          

poiché
                                 .

Nel modello della camminata, come mostra la figura precedente, possiamo osservare un percorso, aa, che conduce a R, uno, bb, che conduce a P e due, ab e ba, che conducono entrambi a Q.
a² rappresenta quindi il percorso che conduce a R, b² quello che conduce a P e 2ab i due percorsi (ab e ba) che conducono a Q.

Anche
                                        

può essere rappresentato sul modello, questa volta contando tre passi del tipo a o b:

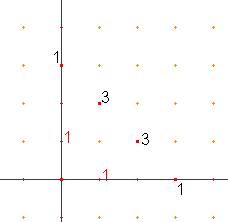
Osservate come i coefficienti del polinomio 1, 3, 3, 1 siano rappresentati ciascuno dal numero dei percorsi che arrivano in un certo punto e le corrispondenti parti letterali dal tipo dei percorsi che confluiscono in quel punto.

In questo modo potete rapidamente calcolare, per esempio,    (a + b)⁷.

3.   Permutazioni o disposizioni semplici
       

Consideriamo 3 palline rosse e 2 blu.
In quanti modi possiamo disporle in fila considerando differenti due permutazioni diversamente ordinate?

Per esempio,   R₁ B₁ B₂ R₃ R₂  ,    R₁ B₂ B₁ R₃ R₂   ,   R₁ R₂ B₁ R₃ B₂    sono da considerarsi permutazioni differenti
(si usa la parola permutazioni per indicare i diversi raggruppamenti ordinati di tutti gli elementi).
 

Invece che elencare tutte le possibilità, lavoro lungo e noioso, seguiamo questa semplice idea, disponendo le palline su uno schema ad albero:

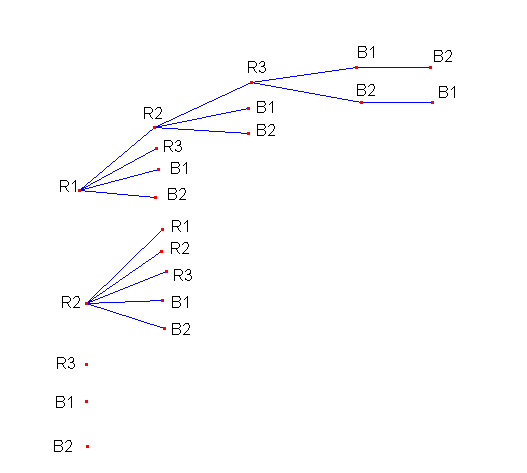
Pensando di completarlo è ora evidente che le palline possono disporsi in  5 · 4 · 3 · 2 = 120  modi o, come anche si dice, sono 120 le permutazioni.

Per il modo in cui è generato, questo numero si indica brevemente con la notazione  5! e si legge 5 fattoriale.

In generale,  n! = n · (n-1) · (n-2)·  ......  · 2 · 1

Una piccola modifica permette di calcolare il numero delle disposizioni delle 5 palline a 3 a 3.
Per esempio,  R₁ B₁ B_{2 ,}     B₁ R₃ R_{2 ,}      R₁ B₂ B_{1 , ...}

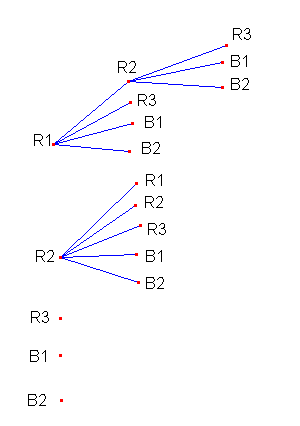
In questo caso il numero si riduce a  5 · 4 · 3 = 60.

4.  Combinazioni semplici

Riprendiamo il caso delle 5 palline, di cui 3 rosse e 2 blu.
Supponiamo che questa volta non ci interessi l'ordine delle palline, ma solo le palline stesse.
Per esempio, riteniamo uguali e contiamo per una le due disposizioni    R₁ B₁ B₂   e   R₁ B₂ B_1.
In tal caso parliamo di combinazioni delle palline.
Quante sono le combinazioni di tali palline, prese a 3 a 3 ?

Osservate il seguente schema:                                              

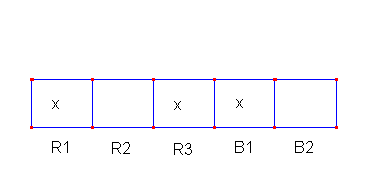
che mostra una possibile combinazione   R₁  R₃  B_{1  .}
Se cambiamo l'ordine di queste tre palline otteniamo 3! disposizioni, ma la combinazione è sempre la stessa;
analogamente, cambiando l'ordine delle palline rimanenti R₂ e B₂, la combinazione resta la stessa.
Si tratta allora di contare le permutazioni di 5 elementi, tenendo conto che da ciascuna di esse se ne ricavano 3! · 2! equivalenti.

Le combinazioni sono quindi  

                                                          .

Questo rapporto è indicato brevemente con la notazione
                                                                              

e si legge  combinazioni di 5 elementi a 3 a 3.

In generale,
                                                        
 

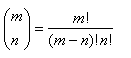
Per indicare questo numero è anche usata la notazione
                                                                             .

Il numero delle combinazioni di  m elementi  n  a  n  è lo stesso di quello delle permutazioni di  m 
elementi, dei quali n sono uguali tra loro e i restanti  m - n  pure uguali fra loro.
Osservate che, se i restanti  m - n sono distinti, il numero di tali permutazioni aumenta a

 (permutazioni, con ripetizione, di m elementi, dei quali solo n sono uguali tra loro).

Con riferimento al modello della camminata, il numero dei percorsi che conducono a M si può rapidamente determinare calcolando le permutazioni, con ripetizione, di 9 lettere, di cui 5 uguali fra loro (le a) e le altre 4 pure uguali fra loro (le b).  Risulta proprio:

                                                         .

In generale, il numero delle permutazioni, con ripetizione, di m elementi, dei quali p uguali fra loro e altri q pure uguali fra loro, ma diversi dai precedenti, sono
                                                                       .

5.  Disposizioni con ripetizione

Pensando di potere ripetere le palline, come nel caso di estrazioni da un'urna rimettendo dentro quelle estratte, occorre contare, nel caso di 5 estrazioni,
le disposizioni con ripetizione del tipo  R₂ R₂ B₁ B₂ B₁ ,  R₁ R₁ R₁ B₂ B_{1,  ...}
Quante siano in tutto si capisce osservando, ancora una volta, il diagramma ad albero, qui sotto riportato solo parzialmente:

                            

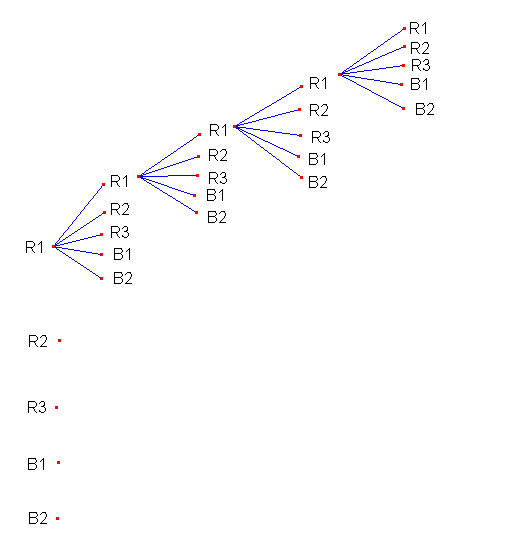
Poiché da ogni ramo ne partono altri cinque, le disposizioni in questione risultano  5⁵ = 3125.

Nel caso, invece, delle disposizioni con ripetizione delle 5 palline a 3 a 3 (caso di 3 estrazioni) si ottiene, analogamente, 5³.

                   .....

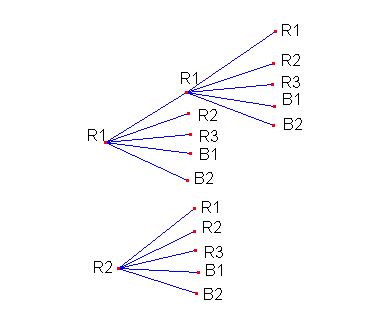
Con riferimento al modello della camminata, i percorsi possibili composti, per esempio, da tre tratti, sono 8, cioè:

                                 aaa,   aab,   aba,   baa,   abb,   bab,   bba,   bbb

Questo risultato si trova addizionando il numero dei percorsi che terminano ai vertici degli isolati sulla terza diagonale (1, 3, 3, 1) oppure calcolando le disposizioni con ripetizione di due lettere a e b, a tre a tre.
 

In generale, le disposizioni con ripetizione di m elementi, a n a n, sono  m ⁿ .
Questo numero si indica anche con la notazione 
                                                                .

6.  Nel modello della camminata osserviamo i percorsi di tre tratti: in base ai punti di arrivo essi si riducono a soli 4 tipi, precisamente  aaa,  aab,  abb,  bbb.
Contare tali percorsi significa contare le combinazioni con ripetizione di due lettere a tre a tre.
Questo numero si indica con la notazione   
                                                               .