Progressioni geometriche e programmazione ricorsiva

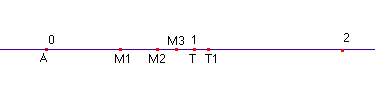
1. Achille, in A,  vuole raggiungere la tartaruga che si trova in T a distanza di 1 metro; parte e corre con la velocità di 1 m/sec, ma quando giunge in T la tartaruga, che avanza alla velocità di 1/10 m/sec, si sarà spostata di un pochino (10 cm), in T1; quando Achille piomba in T1, la tartaruga si sarà spostata, anche se solo di pochissimo, in un punto più avanti T2 ... dunque Achille non riuscirà mai a raggiungere la tartaruga?

Questo paradosso lo formulò Zenone, circa 2500 anni fa.

Naturalmente è evidente che Achille raggiunge la tartaruga, ma come interpretare matematicamente il problema?

La tartaruga viaggia con la legge  del moto  y = 1/10 x +1, mentre Achille con la legge y = x, dove x rappresenta il tempo e y lo spazio percorso (le origini del tempo e dello spazio sono fissate in A).

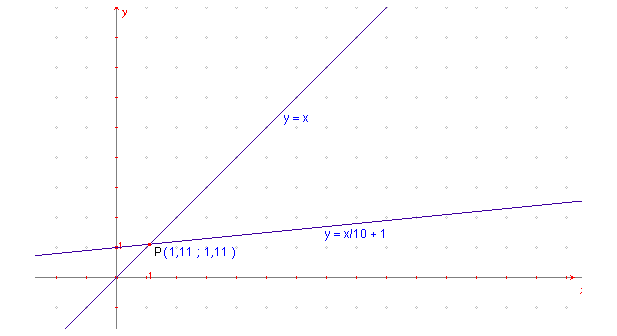
Risolvendo il sistema troviamo  x = y = 10/9 ~ 1,11.

Quindi si incontrano dopo 10/9 secondi, alla distanza di 10/9 metri da A.

D'altra parte, per raggiungere la tartaruga, Achille deve percorrere gli spazi

                             
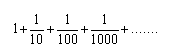
la cui somma deve risultare una distanza finita, che indichiamo con s;

infatti, moltiplicando 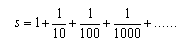   per 1/10, si ottiene:

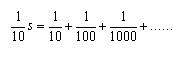
vale a dire, sottraendo la seconda dalla prima:

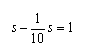
da cui, proprio

                            .

Questi spazi vengono percorsi con una serie di temp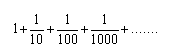i  ,  che diminuiscono anch'essi in ragione di 1/10 uno dall'altro, in modo che la somma totale ci fornisce ancora 10/9 secondi.

Si è così data un'interpretazione matematica che funziona, cioè che permette di spiegare il fenomeno; ma rimane aperto un interrogativo: in qual senso è corretto moltiplicare una serie infinita per 1/10 e dire che si ottiene 1/10 del "valore di partenza"?

                     
Una serie di numeri del tipo precedente, tale che il rapporto tra due termini consecutivi è costante, si dice progressione geometrica.

2. Un programma ricorsivo richiama se stesso  fino ad arrivare ad una informazione nota, per poi risalire alla richiesta dell'utente.
Per esempio, un programma ricorsivo per calcolare la somma dei primi n numeri naturali (problema del piccolo Gauss) può essere il seguente:

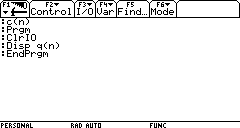
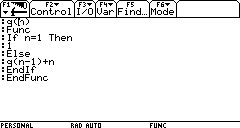
dove il programma principale c richiama la funzione ricorsiva q.

Questo tipo di programmazione utilizza però molta memoria nel calcolatore e non riesce quindi a calcolare c(100).

Verificare fino a quale somma il programma è in grado di calcolare.

Simulare il procedimento ricorsivo con n = 4.

3. Il seguente programma ricorsivo stampa l'n-esimo numero naturale:

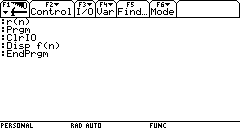
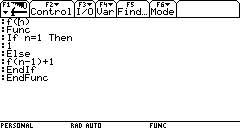
Verificare.

4. Il seguente programma stampa l'n-esimo termine della successione relativa al problema di Achille:

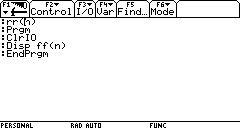
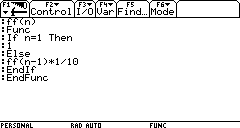
Si riesce a calcolare il 37° termine?

5. Il programma seguente stampa la somma dei primi n termini della successione relativa al problema di Achille:

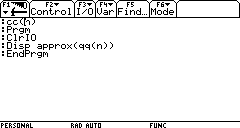
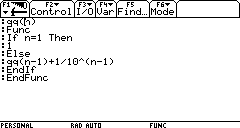
 Si riesce, in questo modo, a calcolare la somma dei primi 43 termini?