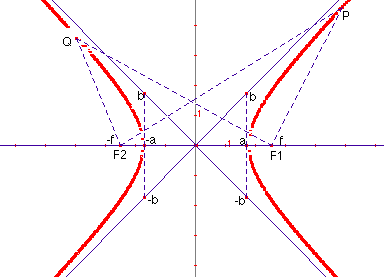
L'iperbole

Un'iperbole è l'insieme dei punti del piano tali che la differenza delle loro distanze da due punti fissi (detti fuochi) è costante.

In figura, PF2 - PF1 = QF1 - QF2 è costante, al variare di P sulla curva; indicando con a la distanza dall'origine delle coordinate del punto P (o Q) quando questo si trova sull'asse x (disposto come in figura, vale a dire, congiungente i fuochi F1 e F2, mentre l'asse y è sistemato perpendicolarmente nel punto medio tra F1 e F2), allora tale differenza può essere indicata con 2a.

L'invarianza della differenza delle distanze, per qualsiasi punto (x;y) dell'iperbole (su un ramo o sull'altro), può essere resa dall'equazione seguente:  

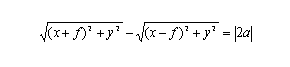
dalla quale, elevando al quadrato e semplificando, si ottiene:

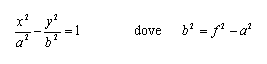
che è l'equazione normale dell'iperbole (con a e b maggiori di zero).

L'iperbole si avvicina, al crescere di x in valore assoluto, sempre più a due determinate rette, senza però mai toccarle, i suoi asintoti.
Per ricercarne le equazioni, si può osservare che risulta, successivamente:

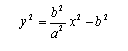
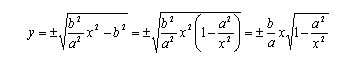
Le pendenze dei due asintoti risultano quindi    e     , ciò che giustifica la figura di cui sopra.

I punti (f;0) e (-f;0) si dicono vertici, ciascuno appartenente a uno dei due  rami di iperbole.
a è il semiasse trasversale, b il semiasse coniugato ed f è la semidistanza focale ().
Il punto medio tra F1 e F2 è il centro dell'iperbole.
La retta passante per i fuochi, contenente quindi il centro, è l'asse trasversale, mentre la sua perpendicolare per il centro è l'asse coniugato (che non interseca l'iperbole).

L'eccentricità di un iperbole 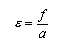   è sempre maggiore di 1.

Un iperbole con asse trasversale l'asse y e vertici i punti (0;a), (0;-a), ha per equazione

                                                                                                               .

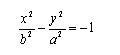Nella figura seguente è riportato un esempio con i due tipi di iperbole.

Le due iperboli si dicono coniugate.

Quali sono le equazioni degli asintoti, nei due casi?

 Un'iperbole particolare

L'iperbole di equazione  , con k > 0,

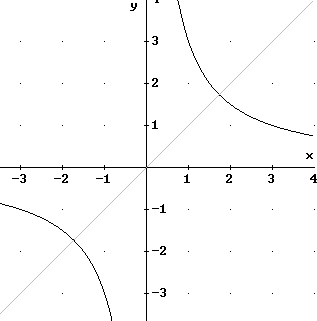
può descrivere una coppia di grandezze inversamente proporzionali.

Sottoponiamo l'iperbole alla rotazione con centro nell'origine delle coordinate e angolo 45° in senso orario, le cui formule sono:

Sostituendo, quindi, le formule inverse

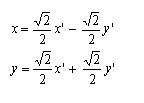
si trova 

ovvero

                                 .

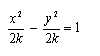L'eccentricità di questa iperbole risulta

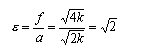
Iperboli di questo tipo, con gli asintoti tra loro perpendicolari (e quindi a = b) si dicono equilatere o rettangolari.
Esse hanno tutte la stessa eccentricità.