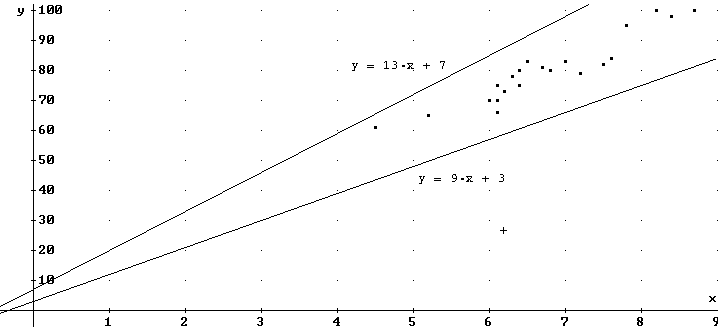
Regressione lineare
 

1. La ricerca dell'equazione della retta che rende minima la somma delle distanze, in valore assoluto, dei punti dati da essa, in uno qualsiasi dei modi possibili (perpendicolarmente, in verticale, in orizzontale) è un primo passo, ma non risulta ottimale.
Pensando, inoltre, di rendere minima la somma delle distanze, per esempio in verticale, prendendole con un segno positivo o negativo, in accordo con il segno della differenza  yp - yr, dove yp è l'ordinata del punto dato e yr quella del punto corrispondente sulla retta, tale somma può tendere a zero, ma la retta modello non risulta unica.
Non si riesce, comunque, utilizzando uno dei metodi suddetti, a determinare, in generale, una formula semplice per calcolare univocamente i parametri a e b della retta modello   y = ax + b.

Invece di minimizzare la somma delle distanze, si può allora provare a minimizzare la somma dei loro quadrati.

La figura dinamica seguente mostra innanzitutto che, considerando a piacere cinque punti A, B, C, D, E, e minimizzando la somma dei quadrati delle loro distanze dalla retta, in verticale, il punto M (mx, my), dove mx è la media delle ascisse e my quella delle ordinate dei dati, appartiene sempre alla retta del modello (muovere i punti e ricercare la retta ottimale).

La retta che minimizza la somma dei quadrati si dice di regressione lineare (o dei minimi quadrati).

2. E' rapido determinare la retta di regressione con un foglio elettronico, o con  Derive.  Provare con il software e l'hardware a disposizione, utilizzando una  qualsiasi tabella di dati.

E' anche possibile determinare l'equazione della retta ottimale progettando un algoritmo opportuno per minimizzare la somma dei quadrati.
Disegnati i punti in un diagramma cartesiano, si possono innanzitutto facilmente determinare (le equazioni di) due rette che li comprendono, come mostra la figura seguente.

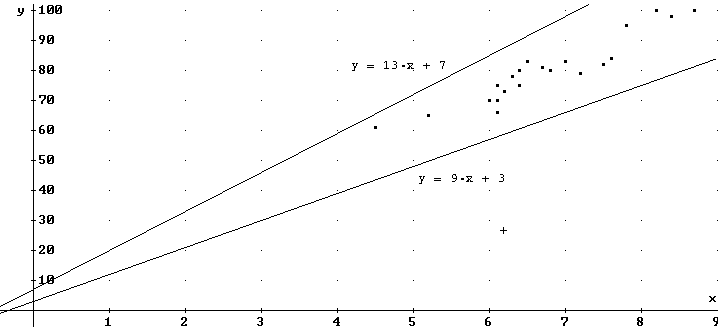
Siano p1, p2 le pendenze e y1, y2 le ordinate determinate dalle rette sull'asse y ( nel nostro caso, p1=13, p2=9, y1=7, y2=3).
L'idea consiste nel cambiare di posizione una generica retta y = a x + b, variando il punto di incontro con l'asse y, fra y1 e y2, e la pendenza, fra p1 e p2; per ogni posizione calcolare la somma dei quadrati, memorizzarla quando risulta più piccola della precedente e, infine, stampare i parametri a, b corrispondenti alla retta per la quale la somma in questione è minore di tutte le altre.

L' algoritmo può essere il seguente:

INTRODUCI IL NUMERO DELLE COPPIE (x,y) DEI DATI, n

RIPETI PER i  DA 1  A  n

        INTRODUCI I DATI x(i), y(i)

0 ----> inizio

INTRODUCI GLI ESTREMI DELLE PENDENZE, p1, p2  (p1 < p2)
INTRODUCI GLI ESTREMI SULL'ASSE y,  y1, y2   (y1 < y2)
INTRODUCI I PASSI DI ELABORAZIONE, p, q

RIPETI PER a DA p1 A p2 CON PASSO p

        RIPETI PER b DA y1 A y2 CON PASSO q

                      RICERCA

STAMPA "retta dei minimi quadrati y = " af " · x + "bf

FINE

dove af e bf sono i parametri finali passati dal sottoprogramma RICERCA, qui sotto riportato:

SOTTOPROGRAMMA RICERCA

0 ----> s

RIPETI PER i DA 1 A n

        (a · x(i) + b - y(i))² + s  ---->  s

SE  inizio = 0  ALLORA

       s  ---->   smin :  a ----> af :   b ---->   bf

FINESE

1 ---->  inizio

SE  s < smin   ALLORA

s ----> smin :  a ----> af :   b ----> bf

FINESE

FINE SOTTOPROGRAMMA

Le variabili x(), y(), inizio, n, a, b, af, bf, smin, devono essere globali.

Si può tradurre l'algoritmo in un programma ed effettuare l'elaborazione, ricavando un'equazione approssimata della retta di regressione (da confrontare con le altre ottenute in modo diverso).

3.  Si può dimostrare che l'equazione della retta di regressione, date le variabili X e Y, è data da:

dove m_x e m_y  sono rispettivamente le medie di X e di Y.