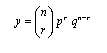
L'equazione della curva normale
 

1. Partiamo dal problema delle palline, con riferimento alla distribuzione binomiale.
Simulando l'esperimento al calcolatore si è visto che le sommità delle barre rettangolari dell'istogramma tendono, con l'aumentare delle prove,a formare una curva a forma di campana.
Scopo del presente lavoro è determinare l'equazione di tale curva.

Indicando con n il numero delle prove, con r quello dei successi in n prove, con p la probabilità di successo e con q quella di insuccesso (p + q = 1), si tratta di studiare la funzione di probabilità, per n tendente all'infinito:

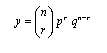
Poiché si deve studiare il limite della funzione, occorre passare dalla variabile discreta r (la cui distribuzione di probabilità è relativa ad un insieme finito di valori) ad una continua (relativa ad un insieme infinito di valori dell'asse reale).
Per questo, è conveniente rappresentare le probabilità dei successi, come si è visto, con le aree dei rettangoli di base 1, in modo da coprire tutto un intervallo reale: ne risulta, in ordinata, una funzione di densità di probabilità.

Nel seguito utilizziamo le notazioni 

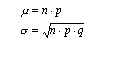
rispettivamente, per il valor medio (atteso) e per la deviazione standard della variabile che esprime il numero dei successi in n prove.
 

Innanzitutto, per semplificare, è opportuno trasformare le coordinate (r, y)  traslando il valor medio nell'origine (0,0) e applicando poi la trasformazione lineare

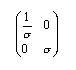
che non altera le aree, essendo il determinante uguale a 1.

Poiché il vettore traslazione è

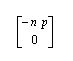
risultano subito le nuove coordinate:

                                                .

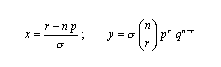Aumentando di 1 la variabile r si ottengono gli incrementi:

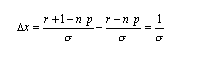
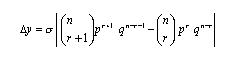
e si capisce subito che

                                          ;

con un software algebrico si può poi confermare l'intuizione sul fatto che  anche ,   all'aumentare di n.

Considerando adesso l'incremento relativo di y, risulta:

                                          .

e si può verificare, ancora con un con un software algebrico, che:

Passando al limite e separando le variabili risulta successivamente::

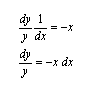
Integrando quest'ultima, si ottiene la funzione:

dove k è una costante positiva.

Poiché si sa che l'area sotto la curva deve valere 1, si può determinare la costante k agevolmente con un software algebrico

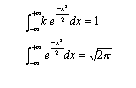
da cui

                 .

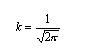L'equazione della forma limite della distribuzione, vale a dire della funzione di densità di probabilità binomiale in questione risulta quindi:                                  

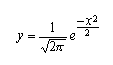
Questa equazione è però riferita, per come abbiamo trasformato le coordinate, a un valor medio uguale a 0 e a una deviazione standard uguale a 1 (curva normale standardizzata).

Disegnando la curva di densità di probabilità in questione con un software algebrico si ottiene la caratteristica forma a campana:

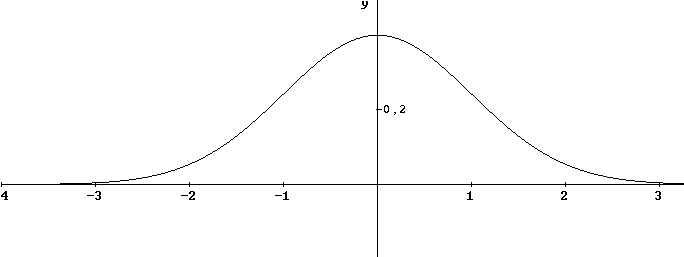
2. Per il caso generale, con m ¹ 0  e  s ¹ 1, ritrasformando la curva nelle condizioni iniziali, si ottiene la seguente funzione di densità di probabilità: 

Questa funzione caratterizza la distribuzione normale (o gaussiana) di una popolazione con valor medio m e deviazione standard s, che descrive il comportamento di molte importanti variabili casuali (per esempio, gli errori casuali di misurazione, il peso di un prodotto, l'altezza dei maschi adulti di un paese).

3.  Nell'ipotesi della distribuzione normale, calcolare la percentuale della popolazione compresa fra

4. Utilizzando la distribuzione normale si può rapidamente trattare, in modo approssimato, il problema dei bambini partecipanti alla festa, che già abbiamo risolto con la distribuzione binomiale.