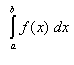Teorema del valor medio per gli integrali definiti

Sia  y = f(x)  una funzione continua in un intervallo chiuso  [a,b], con a < b.

Pensando di calcolare l'area delimitata dalla curva corrispondente e dall'asse delle x, utilizzando il metodo dei trapezi e aumentando il numero delle divisioni dell'intervallo,  si possono ottenere valori sempre più precisi.

Indichiamo il valore esatto dell'area sottesa dalla curva  f(x), tra  a  e  b,  con il simbolo 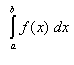     ,  che si dice integrale definito della funzione f(x) nell'intervallo [a.b].

Poiché la funzione è continua, deve avere un valore minimo m e un valore massimo M nell'intervallo, per cui possiamo scrivere:

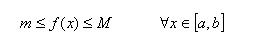
Deve essere allora:

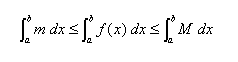
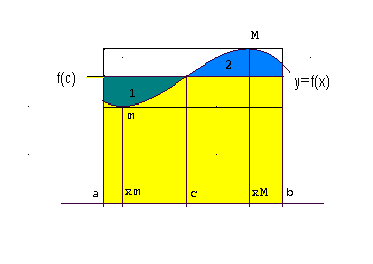
vale a dire, l'area delimitata dalla curva è compresa tra quella del rettangolo di dimensioni m e b-a  (minore) e quella del rettangolo di dimensioni M e b-a (maggiore).

In altri termini:

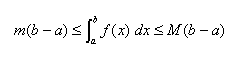
o anche

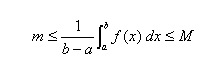
dove                                      .

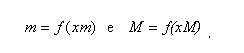La funzione  f(x), continua,  deve però assumere ogni valore compreso tra m ed M, per cui deve esistere un numero c compreso fra xm e xM (e quindi fra a e b) tale che 

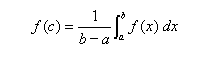
uguaglianza che può anche essere scritta sotto la forma

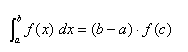
Questo risultato è noto come teorema del valor medio per gli integrali definiti, il nome come conseguenza del fatto che le aree sopra e sotto la retta y = f(c), limitate dalla funzione f(x), sono tra loro uguali (area 1 = area 2).