Studio di funzioni

 

Ricordiamo, innanzitutto, alcuni concetti fondamentali:

un sottoinsieme dei numeri reali che contiene almeno due numeri e, inoltre, tutti i numeri reali compresi fra due qualsiasi dei suoi elementi, si dice che costituisce un intervallo della retta reale;

un intervallo limitato aperto (non contenente gli estremi), con centro un dato punto, costituisce un intorno del punto;

per dominio di una funzione si intende il suo insieme di definizione, vale a dire, l'insieme dei valori della variabile indipendente x per i quali essa risulta calcolabile (detto anche campo di esistenza).

Alcuni punti assumono particolare importanza nello studio del grafico di una funzione.
In particolare, distinguiamo i tre tipi seguenti:

punti stazionari,    per i quali  f ' (x) = 0;

punti singolari,      per i quali f(x) è definita, ma non f '(x);

punti estremi del dominio, quelli che non appartengono ad alcun intervallo aperto contenuto nel dominio.

Essi possono presentare i valori estremi della funzione, vale a dire massimo o minimo assoluti o valori estremi locali, vale a dire massimi o minimi relativi, ma non necessariamente presentano tali valori.

Comunque, se il dominio di una funzione f è un intervallo limitato e chiuso (o unione di tali intervalli) e se f è continua in tale dominio, allora f deve avere in esso un valore massimo e un valore minimo assoluti.

La conoscenza della posizione di questi punti può aiutare a capire il corretto andamento del grafico di una funzione.

Le funzioni si possono classificare in algebriche o trascendenti.

Quelle algebriche si dicono razionali quando risultano esprimibili sotto forma di polinomi (o di rapporti tra essi), irrazionali quando la variabile indipendente
appare sotto il segno di radice.
Negli altri casi si parla di funzioni trascendenti.

E' opportuno, quando possibile, effettuare i seguenti passi, relativamente allo studio del grafico di una funzione y = f(x):

Ecco alcuni esempi (che si possono completare in base alle osservazioni precedenti).

I.  Studio del grafico della funzione               .

La funzione, definita su tutto l'asse reale (il dominio è R), è una funzione pari (simmetrica rispetto all'asse y) e taglia l'asse x nei punti -1, 0, 1, per i quali si annulla il numeratore  della frazione (e, contemporaneamente, non il denominatore).

Dividendo numeratore e denominatore per  x4   si ottiene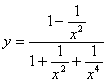                         

        

e si capisce che, per x tendente a infinito, i valori della funzione tendono a 1.
La retta  y = 1  è un asintoto orizzontale.

Per lo studio dei punti stazionari occorre azzerare la derivata prima, ovvero 


                                                          .
 

Risulta quindi  y' = 0  per i valori di x:       
 

                                      
 

Il primo rappresenta un massimo (la derivata prima è positiva a sinistra e negativa a destra), mentre il secondo e il terzo due minimi.

E' ora facile congetturare o verificare il grafico della funzione in questione:

 

                                        
 

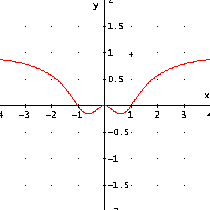
II.   Studio del grafico della funzione     .

Risulta innanzitutto    ,  vale a dire la retta  y = 0 è un asintoto orizzontale.

Ci sono anche due asintoti verticali, per i valori di x  0 e 1 (che annullano il denominatore).

La derivata prima risulta        e si annulla per  

dove è presente un massimo (si può capire studiando la variazione del segno della derivata in un intorno del punto).

Essendoci un massimo in tale punto,  si può verificare se la funzione è simmetrica rispetto alla retta  verticale,  passante per esso,    .

Le formule della simmetria sono:
                                                     

e, come si vede sostituendo le variabili x, y, si ottiene ancora la stessa equazione, il che prova la simmetria in questione.

Studiamo ora che cosa accade quando il valore della x si avvicina a 1 da destra.
Intuitivamente, poiché il numeratore è sempre positivo e il denominatore risulta anch'esso positivo, pur divenendo via via più piccolo, il  valore della frazione tende  a  + ∞.
Precisamente, dimostriamo che  il   

                                                   .

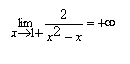Considerato un numero M > 0 grande quanto si vuole, ovvero un intorno di + ∞, risulta successivamente:  

                             

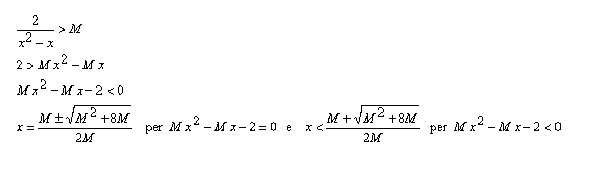
vale a dire, per tutti i valori di x che soddisfano la condizione (intorno destro di 1)

                                            

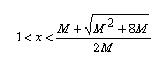
il valore della funzione è compreso nell'intorno di  + ∞ considerato inizialmente.

Per esempio, fissato  M = 100, è sufficiente prendere   x < 1.01962  (fate alcune prove per verificare l'affermazione: che cosa accade per x = 1.018, che cosa per  x = 1.02, ...?).

Stabilite i limiti cui tende la funzione nell'intorno sinistro di 1 e negli intorni (destro e sinistro) di 0.

Visualizzate il grafico al calcolatore, cambiando opportunamente le scale per coglierne le caratteristiche essenziali (andamento in prossimità degli asintoti, punto di massimo).

Il grafico è il seguente:

                                               

                                                  

 

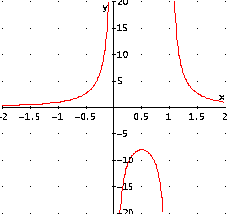
III.   Studio del grafico della funzione              .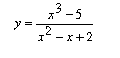

Poiché il grado del numeratore non è minore di quello del denominatore, effettuiamo la divisione tra i polinomi.
Risulta:

                                  

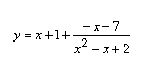
Si capisce subito, quindi, che un asintoto obliquo della funzione è dato dalla retta   y = x + 1.

Calcoliamo le derivate prima e seconda:

                                  

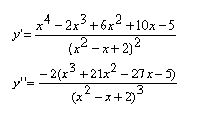
La y' si annulla nei due punti  x ≈ 0.41  e   x  ≈ -1.32, dove sono presenti, rispettivamente, un massimo e un minimo relativi.

La y'' si annulla  nei punti  x  ≈ 1.37,    x  ≈ -0.16,   x  ≈ -22.2 ( cambiando segno negli intorni) e ci informa, quindi, che in tali punti sono presenti dei flessi.

L'asse y è intersecato nel punto x = -2.5, l'asse x nel punto x ≈  1.7.

Il grafico risulta quindi il seguente:

                                                             

 

                                                                   

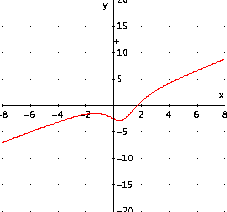
Osservate la variazione del grafico cambiando solo +2  in -2 nel denominatore della frazione e studiate la funzione corrispondente:
                                                 

                                                             

      

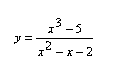
In base a quanto precede (e ad altri esempi analoghi), è possibile affermare che, per una funzione razionale:

- annullando il denominatore si trovano gli asintoti verticali;
- se il grado del numeratore è inferiore a quello del denominatore l'asse x è un
   asintoto orizzontale;
-  se i gradi sono uguali allora  y = k è un asintoto orizzontale (dove k è il rapporto
   dei coefficienti dei monomi di grado maggiore);
- se il grado del numeratore supera di 1 quello del denominatore allora  y = a x + b
   è un asintoto obliquo (determinato dalla divisione dei due polinomi);
- negli altri casi il grafico non ha asintoti rettilinei (ma può avere curve
  asintotiche)                                                                   

 

Studiamo, adesso, qualche funzione non razionale.

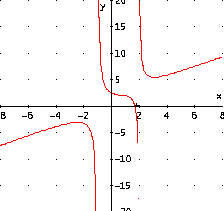
IV.  Studio del grafico della funzione:

                                                      

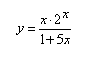
Si capisce subito che c'è un asintoto verticale per  x = - 1/5 e che la curva incontra gli assi nell'origine (0,0) delle coordinate.

Risulta poi:

                              

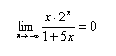
come si vede applicando il teorema di de l'Hospital. 

                            

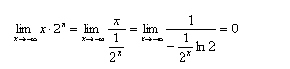
Inoltre:

                              
perchè  (sempre per il suddetto teorema)      .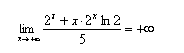

Nell'intorno del punto x = - 1/5 risulta invece:

a sinistra 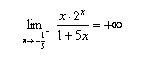        e   a destra       .

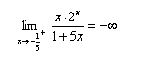Poiché la derivata prima non si annulla mai, non sono presenti massimi o minimi relativi.

Rimane da studiare in modo più preciso il comportamento del grafico per x che tende a  + ∞.

La derivata seconda si annulla per x ≈ 0.593 e si capisce, infine, che in tale punto è presente un flesso.

Il grafico è dunque il seguente: