Ricordando la forma della matrice di una similitudine lineare diretta
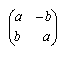 ,
,
consideriamo la corrispondenza biunivoca
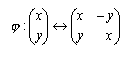
che a ogni punto
![]() del piano diverso da
del piano diverso da
![]() associa la matrice
associa la matrice
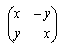 ,
vale a
dire la similitudine che trasforma il punto
,
vale a
dire la similitudine che trasforma il punto
![]() nel punto
nel punto
![]() .
.
Poiché il punto può riguardarsi come rappresentante di un vettore, già sappiamo addizionare, in questo senso, due punti:
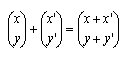
Sappiamo anche addizionare e moltiplicare, in un certo senso, due matrici (completa le uguaglianze seguenti):
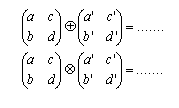
Nelle ipotesi precedenti , poiché
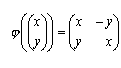
risulta subito che
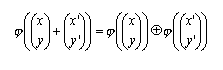
Non abbiamo finora, però, dato alcun
significato alla moltiplicazione dei punti.
Possiamo tentare allora di procedere come segue: prima troviamo le matrici
corrispondenti
ai punti fattori, le moltiplichiamo fra loro e quindi
consideriamo tale risultato come immagine
del prodotto dei punti, vale a dire,
consideriamo come prodotto dei punti la controimmagine
del
prodotto ottenuto fra le matrici corrispondenti.
Così, dati i punti:
![]() e
e
![]() ,
,
risulta
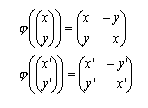
e quindi
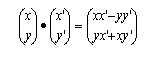
dalla prima colonna della matrice prodotto.
In definitiva
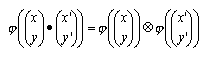
L'insieme dei punti
![]() e delle matrici
e delle matrici
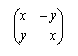 , con le operazioni di
addizione e moltiplicazioni definite,
costituiscono due strutture algebriche,
dove la corrispondenza biunivoca j , che mantiene da
una struttura
all'altra, nel senso di cui sopra, le due operazioni, risulta un
isomorfismo fra le strutture (le due strutture sono isomorfe, vale
a dire, si comportano allo stesso modo dal punto di vista algebrico).
, con le operazioni di
addizione e moltiplicazioni definite,
costituiscono due strutture algebriche,
dove la corrispondenza biunivoca j , che mantiene da
una struttura
all'altra, nel senso di cui sopra, le due operazioni, risulta un
isomorfismo fra le strutture (le due strutture sono isomorfe, vale
a dire, si comportano allo stesso modo dal punto di vista algebrico).
Per brevità, indichiamo con
![]() l'immagine del punto
l'immagine del punto
![]() nella corrispondenza
nella corrispondenza
![]() , quando questa
notazione non comporta
ambiguità di interpretazione.
, quando questa
notazione non comporta
ambiguità di interpretazione.
Risulta, in base a quanto precede,
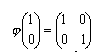 , dove la matrice a secondo membro è
l'identità nella
moltiplicazione fra matrici (elemento neutro), mentre il
punto a primo membro è l'identità nella moltiplicazione
dei punti (appena
definita). Poiché questi due oggetti matematici (matrici e punti) si
comportano, come si è
detto, allo stesso modo, possiamo indicarli entrambi con
la lettera I.
, dove la matrice a secondo membro è
l'identità nella
moltiplicazione fra matrici (elemento neutro), mentre il
punto a primo membro è l'identità nella moltiplicazione
dei punti (appena
definita). Poiché questi due oggetti matematici (matrici e punti) si
comportano, come si è
detto, allo stesso modo, possiamo indicarli entrambi con
la lettera I.
Se indichiamo con -I la matrice (opposta di I):
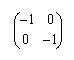
allora risulta
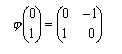 e
e
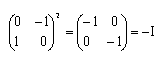
Indicando, inoltre, il punto
![]() e la matrice
e la matrice
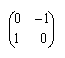 , corrispondenti nell'isomorfismo, con
la lettera i,
possiamo scrivere allora
i2=-I.
, corrispondenti nell'isomorfismo, con
la lettera i,
possiamo scrivere allora
i2=-I.
Indicando ora un generico punto del piano
![]() e la matrice corrispondente
e la matrice corrispondente
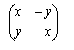 con
la lettera v, possiamo osservare che v può ottenersi
combinando I e i nel modo seguente:
con
la lettera v, possiamo osservare che v può ottenersi
combinando I e i nel modo seguente:
dove a, b sono due opportuni numeri reali.
Ancora, in virtù dell'isomorfismo
fra i numeri reali x e l'insieme dei punti
![]() , indicando I con 1, si
ottiene:
, indicando I con 1, si
ottiene:
v = a + i b
dove i2=-1.
In definitiva, i simboli come v, di cui
i punti del piano e le matrici precedenti costituiscono due
interpretazioni
(con le operazioni dianzi definite), prendono il nome di
numeri complessi.
Si ha essenzialmente una sola struttura, quella dei numeri complessi,
della quale i punti e le matrici costituiscono
due modelli.
In base a quanto precede i numeri complessi si possono addizionare o moltiplicare secondo le ordinarie regole di calcolo valide per i reali, cui si sottomette anche il simbolo i, tenendo solo presente che i2=-1.