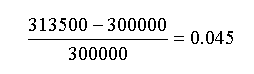
1. La popolazione di una città è cresciuta, nel corso di cinque anni, come mostra la tabella seguente:
 

1° anno        300000            313500

2° anno        313500            327607

3° anno        327607            342349

4° anno        342349            357755

5° anno        357755            373854

Supponendo costante la percentuale di crescita, dopo quanti anni si può prevedere che la popolazione raggiunga 500000 unità?
Per qualsiasi valore del tempo, qual é la corrispondente popolazione?

Poiché             
                

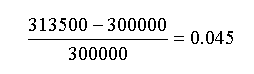
la percentuale di crescita è approssimativamente del 4.5%.

Osserviamo che la popolazione è data da

dopo il 1° anno            300000 + 0.045 · 300000 = 300000 (1 + 0.045)

dopo il 2° anno            300000 (1 + 0.045) + 0.045 · 300000 (1 + 0.045) = 300000 (1+ 0.045)²

dopo il 3° anno            300000 (1+ 0.045)³

          ^{...                                       ...}

ovvero, dopo x anni,       300000 (1+ 0.045)^x =  300000 (1.045)^x.

Per qualsiasi valore del tempo x (in anni), la popolazione corrispondente, dunque, risulta 300000 (1.045)^x.
 

Essa raggiunge, quindi, 500000 unità quando  500000 = 300000 (1.045)^x.

Ricercate, approssimativamente, il valore del tempo x in questione utilizzando una calcolatrice.

2. Ricerca delle leggi a partire dai dati sperimentali
 

Un altro approccio al problema della popolazione è quello di notare che, considerata la tabella

                        1            313500
                        2            327607
                        3            342349
                        4            357755
                        5            373854
 

i punti di coordinate

                             (1, log 313500)
                             (2, log 327607)
                             (3, log 342349)
                             (4, log 357755)
                             (5, log 373854)

dove con log x abbiamo indicato il logaritmo, in una qualsiasi base, del numero x della seconda colonna, risultano allineati.

Per esempio, utilizzando un foglio elettronico (nella colonna C sono considerati i  logaritmi in base 10 dei numeri della colonna p), si vede subito l'allineamento dei punti:

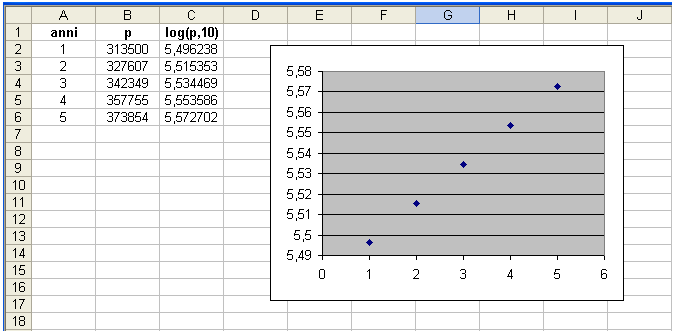
I punti in questione individuano infatti la retta la cui equazione è riportata, approssimativamente, sul grafico:

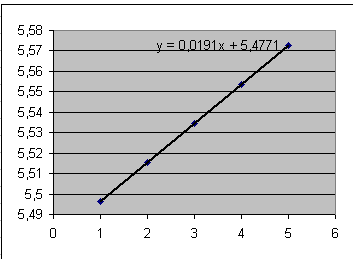
Questo fatto implica che la crescita della popolazione, in funzione del tempo, sia di tipo esponenziale e data dalla formula

                                                                               y = b · a ^x.

Infatti, se consideriamo i logaritmi di entrambi i membri, otteniamo:

                                    log y = log b + x log a

che possiamo anche scrivere come

                                        Y = n + x m

dove, nel nuovo sistema X,Y di assi cartesiani, X = x e Y = log y  (scala logaritmica) e i parametri m, n della retta possono essere determinati dall'equazione della retta.

Precisamente (avendo considerato uguale a 10 la base dei logaritmi):

               m = log₁₀ a          da cui            a = 10^m = 10^0.0191 » 1.045

              n  = log₁₀ b           da cui            b = 10ⁿ = 10^5.4771 »  300000

il che permette di risalire, approssimativamente, alla legge di crescita della popolazione del nostro problema

                                                                           y = 300000 · 1.045^x

Considerando invece i logaritmi di entrambe le colonne, i  punti di coordinate

                             (  x   ,         y      )

                             (log 1,   log 313500)
                             (log 2,   log 327607)
                             (log 3,   log 342349)
                             (log 4,   log 357755)
                             (log 5,   log 373854)

non risultano allineati.

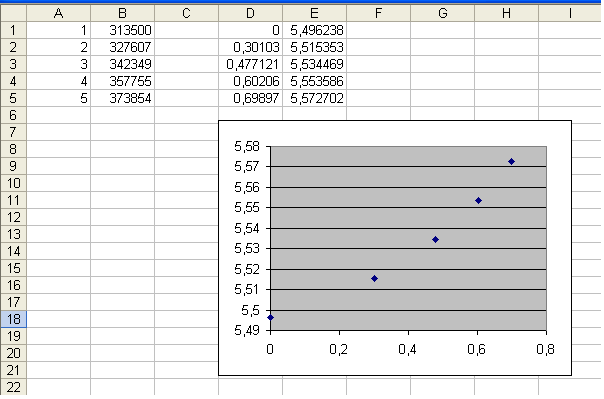
Questo fatto si può constatare rapidamente nel grafico di cui sopra, dove i logaritmi dei dati  x, y sono calcolati nelle colonne D e E.

In questo caso (logaritmi calcolati sui dati di  entrambe le colonne), l'allineamento comporterebbe una legge di potenza, anziché esponenziale.
Infatti, dall'uguaglianza 
                                         y = b · x ^a

risulta subito

                                         log y = log b + a log x

                                     Y = n + m X

vale a dire, sono i punti (log x, log y) ad essere su di una retta, la cui pendenza esprime immediatamente il parametro a.
 

Talvolta i punti  risultano solo approssimativamente allineati e allora può essere opportuno ricercare la "migliore" retta che passa fra di essi (retta di regressione).
La scelta di due punti opportuni (che rappresentino l'andamento dell'insieme) può risultare utile in molti casi, dove non è necessaria una grande precisione.
Per arrivare però a scrivere con sicurezza l'equazione della retta ottimale occorre un altro punto di vista.
Precisamente, si può cercare la posizione della retta che minimizza la somma dei quadrati delle distanze, in verticale, di tutti i punti da essa.

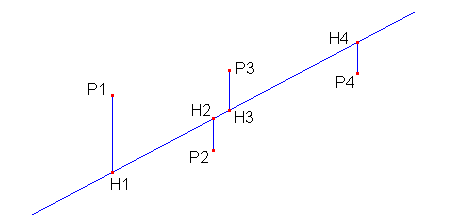
In altri termini, si cerca di  rendere più piccola possibile la somma  (P1H1)² + (P2H2)² + (P3H3)² + (P4H4)² ...

Riprendiamo, per esempio, in considerazione i punti

                                                    (1, log 313500)
                                                    (2, log 327607)
                                                    (3, log 342349)
                                                    (4, log 357755)
                                                    (5, log 373854)

ovvero, approssimando a meno di 1/1000 i logaritmi in base 10,

                                                    (1, 5,496)            
                                                    (2, 5,515)
                                                    (3, 5,534)
                                                    (4, 5,553)
                                                    (5, 5,573)

Indicando con  y = m x + n   l'equazione della retta in questione, la funzione da rendere minima risulta allora la seguente:

f = (5,496 - m·1 - n)² + (5,515 - m·2 - n)² + (5,534 - m·3 - n)² + (5,553 - m·4 - n)² + (5,573 - m·5 - n)² =

  =  55 m² + 30 m·n -166,41 m + 5 n² - 55,342 n + 153,14

Se evidenziamo la variabile m, la funzione

                            f (m) = 55 m² + (30 n - 166,41) m + 5 n² - 55,342 n + 153,14

si può riguardare, pensando  n come  un valore fissato, come funzione della sola m.
In tal caso, poiché essa rappresenta una parabola volta verso l'alto, in corrispondenza del vertice si ottiene il suo minimo valore, vale a dire, per

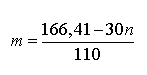
D'altra parte, fissando m si ottiene:

                             f (n) = 5 n² + (30 m - 55,342) n + 55 m² - 166,41 m + 153,14

e questa volta il minimo si ottiene per                                                              

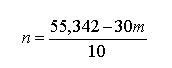
I valori di m e n che soddisfano entrambe le equazioni si possono facilmente determinare risolvendo il sistema:

                                m = 0.0192              ;           n = 5.4766

e, come ci si poteva aspettare, ritroviamo i parametri dati dal foglio elettronico.
 

La retta "migliore" può essere determinata anche con altri metodi.

3. Altri modelli

I.   Logistico

Il modello in questione prevede limitazioni nella crescita o decrescita di una popolazione.

Supponiamo, per esempio, che, in un certo paese, si propaghi un'infezione da virus e siano stati raccolti i seguenti dati, dove x rappresenta il tempo trascorso in ore e y il numero di individui infettati in tale periodo:

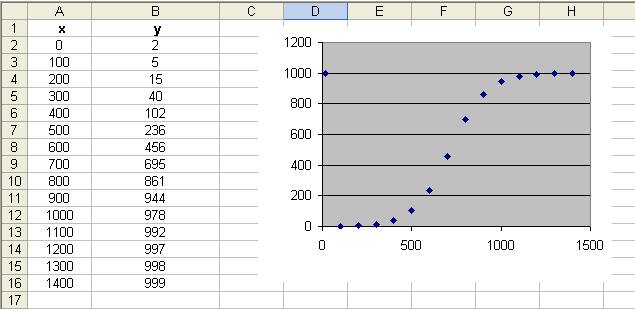
Con un software algebrico possiamo ricercare rapidamente l'equazione della curva che meglio approssima i dati, trovando approssimativamente la seguente:       

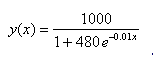
Una funzione del tipo precedente, ovvero

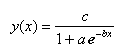
è detta logistica e descrive bene una crescita esponenziale con limitazioni. 

Come si vede dal grafico, in prossimità del valore x = 600 risulta un cambiamento di tendenza nell'andamento della curva, la quale cresce sempre più lentamente, tendendo  a stabilizzarsi al limite rappresentato da c.
Il punto preciso che determina l'inversione di tendenza è un punto di flesso della curva.              

   II.  Logaritmico          
 

In un certo paese di campagna sono state fatte osservazioni, per un arco di 6 anni, sulla crescita del numero di automobili.
La tabella seguente illustra la situazione: al 1° mese le auto contate sono 100, al 3° mese 103, al 6° 105, ..., al 72° 113.
Rappresentando la funzione graficamente, per esempio con un foglio elettronico, l'andamento sembra di tipo logaritmico.

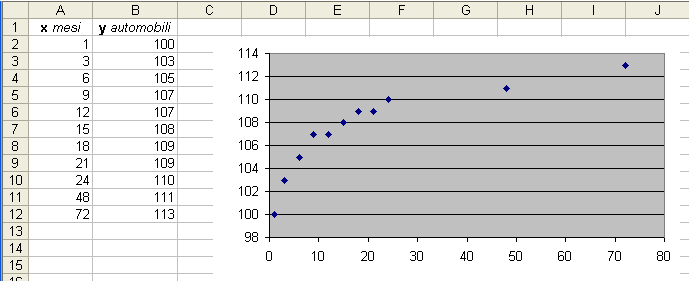
Se, infatti, aggiungiamo una linea di tendenza di questo tipo (tasto destro del mouse sui punti del grafico) otteniamo il risultato seguente:  
                              
           

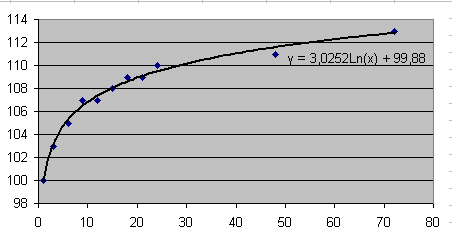
e si vede che la curva approssima molto bene i dati sperimentali.

Dal punto di vista teorico, questo modello può essere rappresentato dalla funzione  y = a + b ln(x).
Quindi, posto X = ln(x), se i punti  (X,y)  risultano allineati è possibile ricavare facilmente i valori dei parametri a e b, anche senza il foglio elettronico o software analoghi.
Infatti, il grafico mostra un discreto allineamento

          

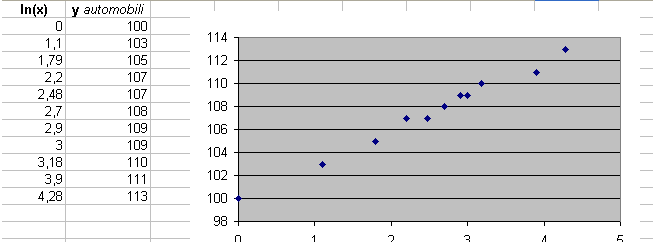
e considerando, per esempio, il secondo (1,1; 103) e l'ultimo punto (4,28; 113) possiamo scrivere l'equazione di una retta  y = a + b X che approssima bene i dati:

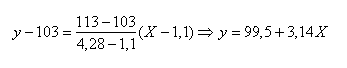
ovvero, approssimativamente,  y = 100 + 3X.

Questo prova che la corrispondenza iniziale  x ---> y  è di tipo logaritmico.

Come già abbiamo visto, la migliore retta che approssima i dati sperimentali può essere determinata in modo preciso con la regressione lineare.

In contesti più significativi il modello logaritmico è adottato, per esempio, in biologia per descrivere la rapidità di crescita relativa, limitata, della misura di una popolazione.

III. Sinusoidale

Il consumo di gas, in metri cubi, da parte di una famiglia, nei mesi da Settembre ad Aprile, in due anni, è stato
il seguente:

mesi                   m³

set-  0                 40
ott-  1                100
nov- 2                250
dic-  3                400
gen- 4                420
feb-  5                360
mar- 6                200
apr-  7                 80
set-  8                 30
ott-  9                120
nov- 10               240
dic-  11               380
gen- 12               390
feb-  13               270
mar- 14               120
apr-  15                30

Questa volta utilizziamo, per esempio, una calcolatrice (TIV) per elaborare i dati.
La rappresentazione grafica è la seguente:

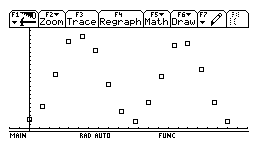
Si intuisce che l'andamento è ciclico, di tipo sinusoidale.

Richiedendo un modello (o, come anche si dice, una regressione) tipo SinReg (tasto F5, calcolo su due variabili) otteniamo infatti subito il risultato e la rappresentazione grafica seguenti:

                         

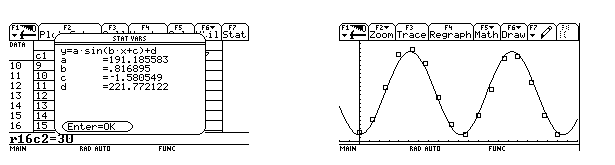
Naturalmente, possiamo arrivare approssimativamente alla stessa conclusione anche senza utilizzare la macchina, impiegando più tempo.
Infatti, partendo dal fatto che l'andamento sia di tipo sinusoidale, si può scrivere inizialmente la funzione

y = sin (x).

Assumendo il periodo uguale a 8, poiché  deve essere 2p / b = 8 segue b ≈ 0.8, ovvero l'equazione diventa

y = sin (0.8 x).

Il grafico è però centrato approssimativamente sulla retta y = 225, per cui l'equazione si modifica in

y = sin (0.8 x) + 225.

Ora, osservando che l'ampiezza delle oscillazioni è circa 195, possiamo ancora modificarla in

y = 195 sin(0.8 x) + 225.

Ci stiamo avvicinando; non rimane che aggiustare la fase:

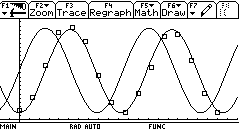
Si capisce che basta traslare la curva verso destra di circa 1.7, per cui l'equazione che ci risulta è, in definitiva,

                        y = 195 sin(0.8 x - 1.7) + 225.

Il grafico seguente mostra la piccola differenza rispetto alla curva ottenuta con la macchina:

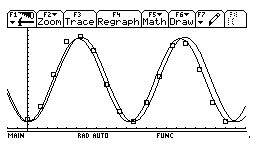
I modelli sinusoidali si adattano bene per fenomeni di tipo ciclico, come la pressione di un'onda sonora nel tempo, la durata della luce diurna nei vari mesi dell'anno, e così via.